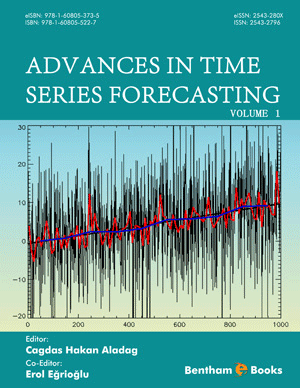
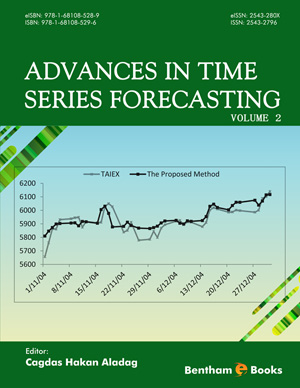
Functions using a Single Variable
Page: 1-9 (9)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010005
PDF Price: $15
Abstract
In this chapter, we will delve into a variety of fundamental subjects related to the study of real functions and the transformations of such functions. To
begin, we will investigate the absolute value, as well as the absolute value function,
and examine the behavior and attributes of each of these concepts. Next, we will
delve deeper into the world of functions, concentrating on the functions that are associated with a single variable and the graphical representations of these functions.
As we move further, we will investigate the most important real-valued functions,
such as polynomial functions and piecewise-defined functions, amongst others. Because of these functions, we are able to acquire a deeper comprehension of transformations and how they have an effect on function graphs. In this lesson, we will
investigate the scaling and translating transformations, focusing on how they affect the features of functions. Examples and activities are presented throughout the
chapter to help readers better understand the fundamental ideas behind graphical
representation and function analysis.
Functions of Several Variables
Page: 10-17 (8)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010006
PDF Price: $15
Abstract
This chapter reviews the real-valued functions on space, with fully
solved examples that show the application and usefulness of their components to
deal with practical problems. Then, we see the types of functions that the reader will
often find in academic and research activities. Later, another family of functions
called Vector-Valued Functions is defined and its usefulness in solving application
problems is shown with examples. Finally, both types of functions are generalized
for higher-dimension spaces.
Probability
Page: 18-29 (12)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010007
PDF Price: $15
Abstract
In this chapter, we delve into the key concepts of probability theory
and the most common statistical distributions. We begin by introducing Bayes’
Theorem and its application in statistical inference. Next, we address the binomial distribution function and its usefulness in analyzing binary events and calculating probabilities. Then, we examine conditional probability and its importance
in decision-making under uncertainty. Subsequently, we immerse ourselves in the
main probabilistic functions, including the normal distribution function and its role
in modeling natural phenomena. Furthermore, we study the Poisson distribution
function, which is applied to situations where the probability of rare events occurring needs to be calculated. Finally, we analyze the general concept of probability
and its interpretation in the context of statistical theory. Additionally, we present
the Total Probability’s Theorem, which allows for the calculation of the probability
of an event based on conditional event information. In summary, this chapter provides a solid foundation for the fundamentals of probability and statistics, exploring
key topics such as Bayes’ Theorem, the binomial distribution function, conditional
probability, main probabilistic functions, the normal distribution function, the Poisson distribution function, probability, and the Total Probability’s Theorem.
Estimation and Decision Theory
Page: 30-44 (15)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010008
PDF Price: $15
Abstract
This chapter covers the basic concepts of inferential statistics and hypothesis testing. The section commences with an explanation of the confidence intervals for the population mean and population standard deviation. Also discussed
are the concepts of cut-off, Type I and Type II errors, false positives, and false negatives. We investigate performance metrics including sensitivity, specificity, true
positive rate, and true negative rate. In addition, receiver operating characteristic
(ROC) curves are introduced and their usefulness in assessing test performance is
emphasized. In addition, binomial and normal distribution tests are discussed. This
chapter provides a solid foundation for comprehending the principles and practical applications of inferential statistics in decision-making and the interpretation of
scientific results.
Non-Parametric Statistic Methods
Page: 45-56 (12)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010009
PDF Price: $15
Abstract
In this chapter, we will explore various methods and statistical tests used
in hypothesis validation and sample comparison. We will begin with an introduction to the formulation of scientific and statistical hypotheses and discuss the determination of the appropriate sample size. Next, we will delve into the analysis
of independent and related samples, examining techniques, such as the one-sample
binomial test, one-sample method, one-sample runs test, two-sample chi-squared
test, two-sample Kolmogorov test, two-sample runs test, and two-sample U test.
These tools will provide researchers and scientists with the ability to rigorously
evaluate their hypotheses and compare samples in a reliable manner.
Correlation Theory
Page: 57-69 (13)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010010
PDF Price: $15
Abstract
In this chapter, we examine the nature of correlations in Euclidean
spaces, focusing on the two-dimensional space R
2
and the three-dimensional space
R
3
. We begin by exploring linear correlations in R
2
, where we analyze calculation
techniques and association measures to quantify the relationship between two continuous variables. Next, we delve into multiple correlations in R
3
, examining how
several variables can be related simultaneously and how their strength and direction
can be jointly measured. Subsequently, we address non-linear correlations in R
2
,
expanding the focus beyond traditional linear relationships. We explore advanced
methods and techniques for detecting and measuring non-linear correlations, allowing us to capture complex and non-linear patterns in the data. Furthermore,
examples of practical applications are discussed where the presence of non-linear
correlations is crucial for analysis and decision-making.
Curve Fitting
Page: 70-83 (14)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010011
PDF Price: $15
Abstract
This chapter presents an overview of curve fitting methods in Euclidean
spaces, with a particular emphasis on R
2 and R
3
. In order to represent linear and
nonlinear interactions between numerous variables, a number of methodologies,
including linear and nonlinear least squares methods, are being investigated. The
linear relationship that exists between two variables is broken down in great detail,
and a broad variety of examples are provided to show how curve fitting methods
can be utilized to build models that are an accurate representation of data sets. In
addition to this, the linear relationship that exists between the three variables under
consideration is dissected, and detailed strategies for dealing with this scenario
are discussed. Curve fitting methods are useful for exploring and evaluating data
in Euclidean spaces, as shown by the results and examples shown below, which
demonstrate the utility and versatility of these methods.
Multivariate Analysis of Variance
Page: 84-97 (14)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010012
PDF Price: $15
Abstract
This chapter examines the analysis of variance (ANOVA) and Fisher
statistical tests as fundamental research methods. Introduction to ANOVA and its
application to the investigation of significant differences between data groups. Subsequently, we examine the application of Fisher tests in various contexts, including one-factor, two-factor, and even three-factor analyses. In addition, we investigate the design and experimental application of Latin squares. We conclude by
discussing multivariate analysis of variance (MANOVA) and emphasizing its usefulness for investigating multiple response variables. This chapter concludes with
a comprehensive overview of the previously mentioned statistical techniques and
their applicability to scientific research.
Discrete-Time Markov Chains
Page: 98-109 (12)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010013
PDF Price: $15
Abstract
In this chapter, we look at how Monte Carlo simulations and the Markov
chain theory can be used to analyze urban transportation problems. Vectors describing the starting and final states of a public transportation network are introduced as
fundamental notions. The transition probability matrix and the stochastic matrix are
investigated as potential tools for modeling the dynamic evolution of urban mobility
using discrete-time Markov Chains. The features of Markov Chains, as revealed by
their eigenvalues and eigenvectors, are examined. The Markov Chain Monte Carlo
technique for statistical sampling and analysis of urban mobility issues is also discussed. The methodologies’ potential utility in urban transportation planning and
decision-making is emphasized. Understanding and addressing the difficulties of
urban mobility are greatly aided by the theoretical and conceptual groundwork laid
out in this chapter.
Solutions
Page: 110-118 (9)
Author: Carlos Polanco*
DOI: 10.2174/9789815223132124010014
PDF Price: $15
Introduction
Fundamentals of Mathematics in Medical Research: Theory and Cases is a comprehensive guide to the mathematical principles and methods used in medical research. This book is structured to facilitate learning and application and gives a solid foundation to readers. The book is divided into multiple parts that explain basic concepts in a progressive way. - Part I covers real-valued functions of one or more variables with geometric representations to establish a core understanding of advanced mathematics - Part II covers inferential methods of probability and statistics from basic probability to parametric and nonparametric tests - Part III covers correlation theory and advanced analysis of real-valued functions - Part IV covers multivariable analysis for solving complex problems with an explanation of Markov Chain models - An Appendix provides solutions for all exercises and along with Fortran 90 programs, Python scripts and Linux scripts to explore the mathematical concepts explained in the book. Key Features: Introduction and Conclusion in Every Chapter Exercises and Solutions Program codes and scripts Comprehensive Coverage of Mathematics for Academics and Research Real-World Cases This book is an essential resource for researchers, students, and professionals in medicine and allied fields who seek to understand and apply mathematical methods in their work.